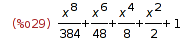AM33 Project 1 Answers using wxMaxima
1 Problem 1
| (%i1) | de: (1+x^2)*'diff(y,x) + x*y - 2 = 0; |
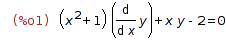
Here's the easy way to solve it, given that Maxima's ode2 is able to solve this equation
| (%i2) | ode2(de,y,x); |
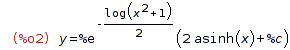
| (%i3) | ic1(%,x=0,y=1); |
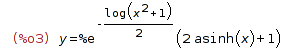
| (%i4) | y_series: taylor(rhs(%),x,0,10); |
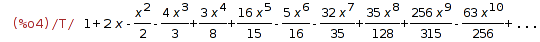
Here's how to solve the recurrence using mhw's enhanced solve_rec package
( not yet included in the standard Maxima distribution,
but available at http://www.netris.org/~mhw/maxima/solve_rec.html )
| (%i5) | load(solve_rec_mhw); |
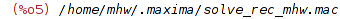
| (%i6) | eq: c[n+1] = -n/(n+1)*c[n-1]; |
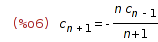
| (%i7) | solve_rec(eq, c[n], c[0]=1, c[1]=2); |
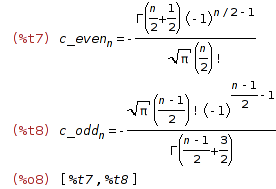
Here's how to do it with Maxima's standard solve_rec package.
We must break the recurrence into two independent recurrences
of order 1: one for the even indices, and one for the odds.
First, we shift the recurrence by 1,
so that even n corresponds to even indices
| (%i9) | load(solve_rec); |
| (%i10) | eq: eq, n=n+1; |
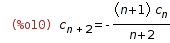
Solve the recurrence for even indices
| (%i11) | eq, n=k*2, c[n]:=ce[n/2], ratsimp; |
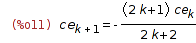
| (%i12) | solve_rec(%, ce[k], ce[0]=1); |
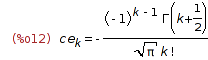
| (%i13) | %, k=n/2, ce[k]:=c[2*k], ratsimp; |
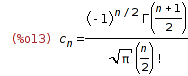
| (%i14) | define(c_even[n], rhs(%)); |
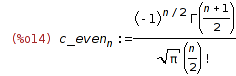
Now solve the recurrence for the odd indices
| (%i15) | eq, n=k*2+1, c[n]:=co[(n-1)/2], ratsimp; |
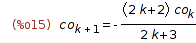
| (%i16) | solve_rec(%, co[k], co[0]=2); |
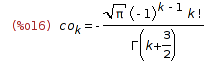
| (%i17) | %, k=(n-1)/2, co[k]:=c[2*k+1], ratsimp; |
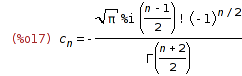
| (%i18) | define(c_odd[n], rhs(%)); |
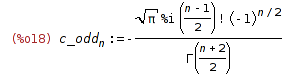
Combine the even and odds into one unified array function
| (%i19) |
c[n] := if evenp(n) then c_even[n] elseif oddp(n) then c_odd[n] else '(c[n])$ |
| (%i20) | makelist(c[n],n,0,10); |
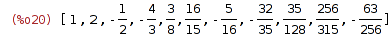
| (%i21) | trunc(sum(c[n]*x^n,n,0,10)); |
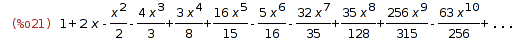
2 Problem 2
| (%i22) | kill(all); |
| (%i1) | Dy: t^2/(y^2-1); |
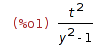
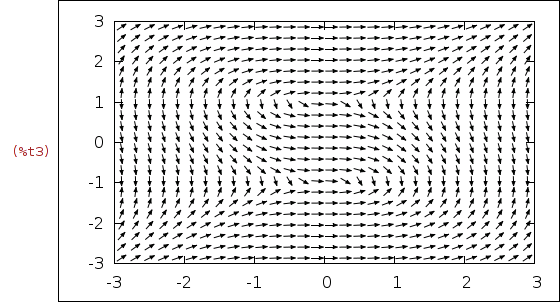
Here we use mhw's drawdf package, which is not yet included in the
standard Maxima distribution, but available at
http://www.netris.org/~mhw/maxima/drawdf-demo.html
You may also use Maxima's standard plotdf package. Use the same
commands given below, but use "plotdf" instead of "wxdrawdf".
| (%i2) | load(drawdf)$ |
| (%i3) | wxdrawdf(Dy, [t,y], [t,-3,3], [y,-3,3])$ |
| (%i4) |
forward_euler(yprime, tvar, yvar, t0, t1, y0, h) := block([t:t0, y:y0, n:round((t1-t0)/h), k1], for i:1 thru n do ( k1:at(yprime, [tvar=t, yvar=y]), y:y+h*k1, t:t+h ), y )$ |
| (%i5) | Dy; |
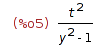
| (%i6) | forward_euler(Dy, t, y, 0, 0.8, 0, 0.02); |
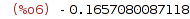
| (%i7) | forward_euler(Dy, t, y, 0, 0.8, 0, 0.01); |
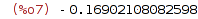
| (%i8) | forward_euler(Dy, t, y, 0, 0.8, 0, 0.005); |
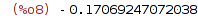
3 Problem 3
| (%i9) | Dy: 3 - 4*t - 2*y/t; |
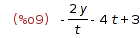
| (%i10) |
backward_euler(yprime, tvar, yvar, t0, t1, y0, h) := block([t:t0, y:y0, n:round((t1-t0)/h)], for i:1 thru n do ( t:t+h, y:find_root(v = y + h*at(yprime, [tvar=t, yvar=v]), v, -1e100, 1e100) ), y )$ |
| (%i11) | backward_euler(Dy, t, y, 1, 2, 2, 0.05); |
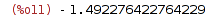
| (%i12) |
improved_euler(yprime, tvar, yvar, t0, t1, y0, h) := block([t:t0, y:y0, n:round((t1-t0)/h), k1, k2], for i:1 thru n do ( k1:at(yprime, [tvar=t, yvar=y]), k2:at(yprime, [tvar=t+h, yvar=y+h*k1]), y:y+h*(k1+k2)/2, t:t+h ), y )$ |
| (%i13) | improved_euler(Dy, t, y, 1, 2, 2, 0.05); |
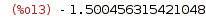
| (%i14) |
modified_euler(yprime, tvar, yvar, t0, t1, y0, h) := block([t:t0, y:y0, n:round((t1-t0)/h), k1, k2], for i:1 thru n do ( k1:at(yprime, [tvar=t, yvar=y]), k2:at(yprime, [tvar=t+h/2, yvar=y+h*k1/2]), y:y+h*k2, t:t+h ), y )$ |
| (%i15) | modified_euler(Dy, t, y, 1, 2, 2, 0.05); |
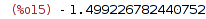
Now we find the exact solution and value at t=2
| (%i16) | ode2('diff(y,t)=Dy, y, t); |
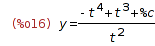
| (%i17) | ic1(%, t=1, y=2); |
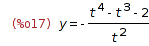
| (%i18) | expand(%); |
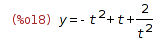
| (%i19) | %, t=2; |

4 Problem 4
| (%i20) | Dy: t^2 + y^2; |
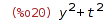
| (%i21) | wxdrawdf(Dy, [t,y], [t,-3,3], [y,-3,3])$ |
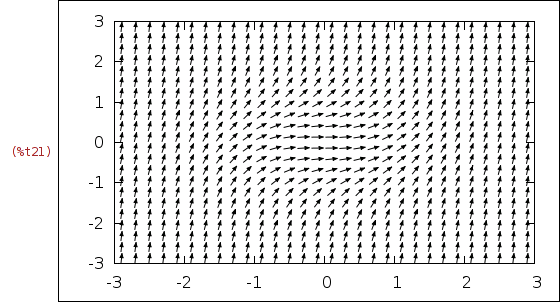
| (%i22) |
predictor_corrector(yprime, tvar, yvar, t0, t1, y0, h) := block([t:t0+h, lasty:y0, y, n:round((t1-t0)/h), k1, ypre, ycorr], y:improved_euler(yprime, tvar, yvar, t0, t, y0, h), for i:2 thru n do ( k1: at(yprime, [tvar=t, yvar=y]), ypre: y + 3*h/2*k1 - h/2*at(yprime, [tvar=t-h, yvar=lasty]), ycorr: y + h/2*k1 + h/2*at(yprime, [tvar=t+h, yvar=ypre]), [lasty,y]:[y,ycorr], t:t+h ), y )$ |
| (%i23) | predictor_corrector(Dy, t, y, 0, 0.5, 0, 0.05); |
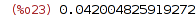
5 Problem 5
| (%i24) |
picard_iter(yprime, xvar, yvar, x0, y0, expr) := y0 + integrate(subst(yvar=expr, yprime), xvar, x0, xvar); |
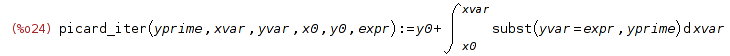
| (%i25) | 1; |
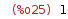
| (%i26) | picard_iter(x*y,x,y,0,1,%), expand; |
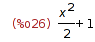
| (%i27) | picard_iter(x*y,x,y,0,1,%), expand; |
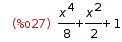
| (%i28) | picard_iter(x*y,x,y,0,1,%), expand; |
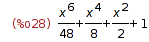
| (%i29) | picard_iter(x*y,x,y,0,1,%), expand; |